Гіпербала (матэматыка)
Шаблон:Універсальная картка Шаблон:Значэнні
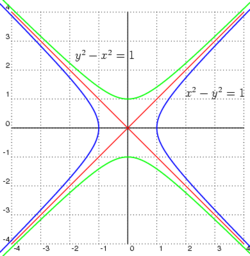
Гіпербала — геаметрычнае месца пунктаў на плоскасці, ад якіх модуль рознасці адлегласцяў да 2 вызначаных кропак (фокусаў) застаецца нязменным.
Гіпербалу, як і эліпс ці парабалу, можна атрымаць праз канічныя сячэнні плоскасцю. У такім разе гіпербалу можна вызначыць як канічнае сячэнне з эксцэнтрысітэтам .
Ураўненні гіпербалы
Кананічнае ўраўненне
Кананічным ураўненнем гіпербалы называецца ўраўненне:
Асімптоты
Асімптотамі гіпербалы называюцца прамыя, якія касаюцца гіпербалы ў бясконца аддаленым пункце. Яны апісваюцца наступнымі ўраўненнямі:
На малюнку яны паказаныя чырвонымі лініямі.
Спасылкі
Шаблон:Крывыя Шаблон:Канічныя сячэнні Шаблон:Бібліяінфармацыя