Гнуткасць стрыжня

Схемы дэфармавання і каэфіцыенты $\mu$ пры розных умовах замацавання і спосабу прыкладання нагрузкі

Гнуткасць стрыжня - стаўленне разліковай даўжыні стрыжня $l_0$ да найменшага радыуса інерцыі $i$ яго папярочнага сячэння.

$\lambda =\frac{l_0}{i}$

Гэты выраз гуляе важную ролю пры праверцы сціснутых стрыжняў на ўстойлівасць. У прыватнасці, ад гнуткасці залежыць каэфіцыент падоўжнага выгібу $\varphi$. Стрыжань з большай гнуткасцю, пры іншых нязменных параметрах, мае больш нізкую трываласць на сціск і сціск з выгібам.

Разліковая даўжыня $l_0$ вылічаецца па формуле:

$l_0=\mu l$, дзе

$\mu$ — каэфіцыент, які залежыць ад умоў замацавання стрыжняў, а $l$ — геаметрычная даўжыня. Разліковая даўжыня, таксама называецца прыведзенай або свабоднай.

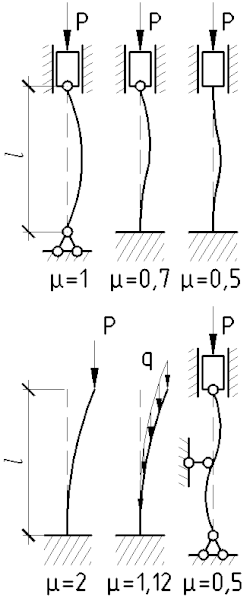
Паняцце прыведзеная даўжыня ўпершыню ўвёў Ясінскі, для абагульнення формулы крытычнай сілы Эйлера, якую той выводзіў для стрыжня з шарнірна-абпертымі канцамі. Адпаведна каэфіцыент $\mu$ роўны пры шарнірных канцах (асноўны выпадак) аднаму, пры адным шарнірнам, другім зашчэмленым $\mu =0.7$, пры абодвух зашчэмленых канцах $\mu =0,5$. Схемы дэфармавання і каэфіцыенты $\mu$ пры розных умовах замацавання і спосабе прыкладання нагрузкі, намаляваныя на малюнку. Таксама, варта адзначыць, што формула Эйлера дакладная толькі для элементаў вялікай гнуткасці, напрыклад для сталі яна ўжываецца пры гнуткасці парадку $\lambda =100$ і вышэй.

Пры разліках элементаў жалезабетонных канструкцый да гнуткасці прад'яўляюцца патрабаванні па яе абмежавання. Таксама, у залежнасці ад гнуткасці прызначаецца велічыня армавання.

У разліках сталёвых канструкцый гнуткасць мае найбольшае значэнне з прычыны вялікай трываласці сталі з вынікаючай з гэтага формай элементаў (доўгія, невялікі плошчы), з-за чаго вычарпанне апорнай здольнасці па ўстойлівасці надыходзіць да вычарпання запасу трываласці па матэрыяле.

Адсюль ўвод дадатковых тэрмінаў:

• Умоўная гнуткасць
• Прыведзеная гнуткасць
• Лімітавая гнуткасць

Існуюць формулы для вызначэння гнуткасці элементаў складовых сячэнняў.

Літаратура

• Сопротивление материалов, Н. М. Беляев, Главная редакция физико-математической литературы изд-ва «Наука», 1976 г., стр 608.
• Металлические конструкции. В 3 т. Т. 1. Элементы стальных конструкций: Учеб. пособие для строит. вузов/В. В. Горев, Б. Ю. Уваров, В. В. Филиппов и др.; Под ред. В. В. Горева. — М.: Высш. шк., 1997. — 527 с.: ил.