Бэта-функцыя

Графік бэта-функцыі пры рэчаісных аргументах

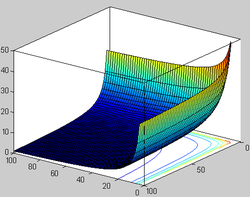
У матэматыцы бэта-функцыяй (Β-функцыяй, бэта-функцыяй Эйлера або Эйлеравым інтэгралам I-га роду) называецца наступная спецыяльная функцыя ад двух зменных:

$\mathrm{B}(x,y)=\underset{0}{\overset{1}{\int }}{t}^{x-1}(1-t{)}^{y-1}dt,$

вызначаная пры $\mathrm{\Re }(x)>0,$ $\mathrm{\Re }(y)>0.$

Бэта-функцыя была даследавана Эйлерам і Лежандрам, А назву ёй даў Жак Бінэ.

Уласцівасці

Бэта-функцыя сіметрычная адносна перастаноўкі зменных, гэта значыць

$\mathrm{B}(x,y)=\mathrm{B}(y,x).$

Бэта-функцыю можна выразіць праз іншыя функцыі:

$\mathrm{B}(x,y)=\frac{\mathrm{\Gamma }(x)\mathrm{\Gamma }(y)}{\mathrm{\Gamma }(x+y)},$

дзе $\mathrm{\Gamma }(x)$ — гама-функцыя;

$\mathrm{B}(x,y)=2\underset{0}{\overset{\pi /2}{\int }}{\sin }^{2x-1}\theta {\cos }^{2y-1}\theta d\theta ,\mathrm{\Re }(x)>0,\mathrm{\Re }(y)>0;$

$\mathrm{B}(x,y)=\underset{0}{\overset{\mathrm{\infty }}{\int }}\frac{t^{x-1}}{(1+t{)}^{x+y}}dt,\mathrm{\Re }(x)>0,\mathrm{\Re }(y)>0;$

$\mathrm{B}(x,y)=\frac{1}{y}\sum _{n=0}^{\mathrm{\infty }}(-1{)}^n\frac{(y{)}_{n+1}}{n!(x+n)},$

дзе $(x{)}_n$ — сыходны фактарыял, роўны $x\cdot (x-1)\cdot (x-2)\cdot \dots \cdot (x-n+1).$

Як гама-функцыя для цэлых лікаў з’яўляецца абагульненнем фактарыяла, так і бэта-функцыя з’яўляецца абагульненнем бінаміяльных каэфіцыентаў з трохі змененымі параметрамі:

${\mathrm{C}}_n^k=\frac{1}{(n+1)\mathrm{B}(n-k+1,k+1)}.$

Вытворныя

Частковыя вытворныя у бэта-функцыі наступныя:

$\frac{\partial }{\partial x}\mathrm{B}(x,y)=\mathrm{B}(x,y)(\frac{{\mathrm{\Gamma }}^{\prime }(x)}{\mathrm{\Gamma }(x)}-\frac{{\mathrm{\Gamma }}^{\prime }(x+y)}{\mathrm{\Gamma }(x+y)})=\mathrm{B}(x,y)(\psi (x)-\psi (x+y)),$

дзе $\psi (x)$ — дыгама-функцыя.

Няпоўная бэта-функцыя

Няпоўная бэта-функцыя — гэта абагульненне бэта-функцыі, якое замяняе інтэграл па адрэзку $[0,1]$ на інтэграл з пераменнай верхняй мяжой:

${\mathrm{B}}_x(a,b)=\underset{0}{\overset{x}{\int }}{t}^{a-1}(1-t{)}^{b-1}dt.$

Пры $x=1$ няпоўная бэта-функцыя супадае з поўнай.

Рэгулярызаваная няпоўная бэта-функцыя

Рэгулярызаваная няпоўная бэта-функцыя вызначаецца праз поўную і няпоўную бэта-функцыі:

$I_x(a,b)=\frac{{\mathrm{B}}_x(a,b)}{\mathrm{B}(a,b)}.$

Уласцівасці рэгулярызаванай няпоўнай бэта-функцыі:

• $I_0(a,b)=0;$
• $I_1(a,b)=1;$
• $I_x(a,b)=1-I_{1-x}(b,a);$
• $I_x(a+1,b)=I_x(a,b)-\frac{x^a(1-x{)}^b}{aB(a,b)}.$

Гл. таксама

• Гама-функцыя

Літаратура

• Шаблон:Кніга

Спасылкі

• Шаблон:MathWorld