Фігуры Лісажу

Фігу́ры Лісажу́ — замкнутыя траекторыі, намаляваныя кропкай, якая здзяйсняе адначасова два гарманічныя ваганні ў двух узаемна перпендыкулярных напрамках. Упершыню даследаваны французскім навукоўцам Жулем Антуанам Лісажу. Выгляд фігур залежыць ад суадносін паміж перыядамі (частотамі), фазамі і амплітудамі абодвух ваганняў. У найпрасцейшым выпадку роўнасці абодвух перыядаў фігуры ўяўляюць сабой эліпсы, які пры рознасці фаз 0 альбо $π$ выраджаюцца ў адрэзкі прамых, а пры рознасці фаз $\frac{π}{2}$ і роўнасці амплітуд ператвараюцца ў акружнасць. Калі перыяды абодвух ваганняў недакладна супадаюць, то рознасць фаз увесь час змяняецца, з прычыны чаго эліпс увесь час дэфармуецца. Пры істотна розных перыядах фігуры Лісажу не назіраюцца. Аднак, калі перыяды суадносяцца як цэлыя лікі, то праз прамежак часу, роўны найменшаму кратнаму абодвух перыядаў, рухомая кропка зноў вяртаецца ў тое ж месца — атрымліваюцца фігуры Лісажу больш складанай формы. Фігуры Лісажу упісваюцца ў прамавугольнік, цэнтр якога супадае з пачаткам каардынат, а бакі паралельныя восям каардынат і змешчаны па абодвух баках ад іх на адлегласцях, роўных амплітудам ваганняў.

Матэматычны выраз для крывой Лісажу

{\begin{matrix} x (t) = A \sin (a t + δ), \\ y (t) = B \sin (b t), \end{matrix}

дзе Шаблон:Math, Шаблон:Math — амплітуды ваганняў, Шаблон:Math, Шаблон:Math — частоты, Шаблон:Math — зрух фаз.

Выгляд крывой істотна залежыць ад суадносін Шаблон:Math. Калі суадносіны роўныя 1, фігура Лісажу мае выгляд эліпса, пры пэўных умовах яна мае выгляд акружнасці (Шаблон:Math, Шаблон:Math радыян) і адрэзка прамой (Шаблон:Math). Яшчэ адзін прыклад фігуры Лісажу — парабала (Шаблон:Math, Шаблон:Math). Пры іншых суадносінах фігуры Лісажу ўяўляюць сабой больш складаныя фігуры, якія з'яўляюцца замкнутымі пры ўмове Шаблон:Math — рацыянальны лік.

Фігуры Лісажу, дзе a = 1, b = N (N — натуральны лік) і

δ = \frac{N - 1}{N} \frac{π}{2}

з'яўляюцца паліномамі Чабышова першага рода ступені N.

Прыклады

Анімацыя ўнізе дэманструе змяненне крывых пры нарастанні суадносін $\frac{a}{b}$ ад 0 да 1 з крокам 0.01. (Шаблон:Math)

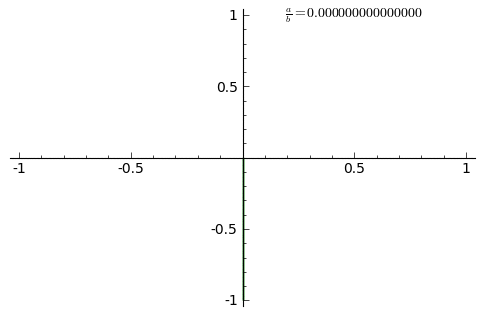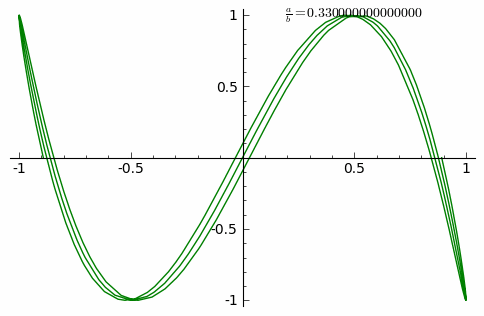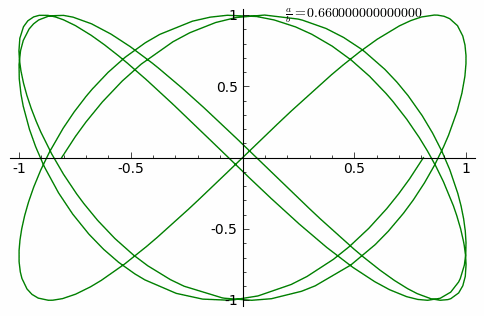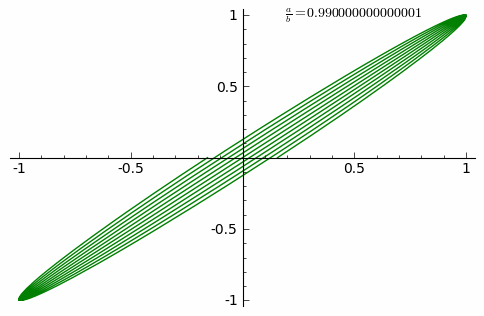
Прыклады фігур Лісажу ніжэй з Шаблон:Math, няцотным натуральным лікам a, і таксама натуральным лікам b, і |a − b| = 1.

Шаблон:Center

Выкарыстанне ў тэхніцы — параўнанне частот

Калі падаць на ўваходы «X» і «Y» асцылографа сігналы блізкіх частот, то на экране можна ўбачыць фігуры Лісажу. Гэты метад шырока ўжываецца для параўнання частот сігналаў дзвюх крыніц і для падстройкі адной крыніцы пад частату другой. Калі частоты блізкія, але не роўныя адна адной, фігура на экране круціцца, прычым перыяд цыкла кручэння з'яўляецца велічынёй, адваротнай рознасці частот, напрыклад, калі перыяд абароту роўны 2 с — розніца ў частотах сігналаў роўная 0,5 Гц. Пры роўнасці частот фігура застаецца нерухомай, у любой фазе, аднак на практыцы, за кошт кароткачасовых нестабільнасцей сігналаў, фігура на экране асцылографа звычайна ледзь-ледзь падрыгвае. Выкарыстоўваць для параўнання можна не толькі аднолькавыя частоты, але і тыя, што знаходзяцца ў кратных суадносінах, напрыклад, калі ўзорная крыніца можа выдаваць частату толькі 5 МГц, а аб'ект наладкі — 2,5 МГц.

Гл. таксама

Літаратура

Справочник по радиоэлектронным устройствам. В 2-х томах; Под ред. Д. П. Линде — М.: Энергия, 1978.
Справочник по физике. Яворский Б. М., Детлаф А. А. — М.: Наука, 1981.

Спасылкі

Шаблон:Крывыя

Шаблон:Rq