Элементы арбіты

Арбітальныя элементы, элементы арбіты нябеснага цела — набор параметраў, якія задаюць памеры і форму арбіты (траекторыі) нябеснага цела, размяшчэнне арбіты ў прасторы і месца размяшчэння нябеснага цела на арбіце.

Вызначэнне арбіт нябесных целаў з’яўляецца адной з задач нябеснай механікі. Для задання арбіты спадарожніка планеты, астэроіда ці Зямлі выкарыстоўваюць так званыя «арбітальныя элементы». Арбітальныя элементы адказваюць за заданне базавай сістэмы каардынат (пункта адліку, восі каардынат), формы і памеру арбіты, яе арыентацыі ў прасторы і момант часу, у які нябеснае цела знаходзіцца ў пэўным пункце арбіты. Галоўным чынам выкарыстоўваюцца два спосабы задання арбіты (пры наяўнасці сістэмы каардынат):

• пры дапамозе вектараў становішча і скорасці;
• пры дапамозе арбітальных элементаў.

Кеплеравы элементы арбіты

Элементы арбіты

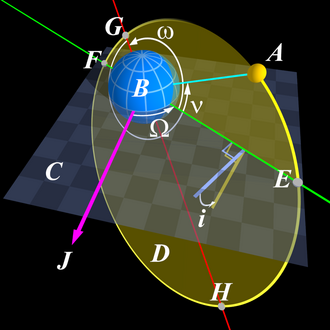
Традыцыйна ў якасці элементаў арбіты выкарыстоўваюць шэсць велічынь, якія атрымалі назву кеплеравых:

• вялікая паўвось (Шаблон:Math);
• эксцэнтрысітэт арбіты (Шаблон:Math);
• нахіленне (Шаблон:Math);
• аргумент перыцэнтра (Шаблон:Math);
• даўгата ўзыходнага вузла (Шаблон:Math);
• сярэдняя анамалія (Шаблон:Math).

Іншыя элементы арбіты

Анамаліі

Анамаліі

Анамалія (у нябеснай механіцы) — вугал, які выкарыстоўваецца для апісання руху цела па эліптычнай арбіце. Тэрмін «анамалія» упершыню ўведзены Адэлардам Бацкім пры перакладзе на латынь астранамічных табліц Аль-Харэзмі «Зідж» для перадачы арабскага тэрміна «аль-хеза» («асаблівасць»).

Сапраўдная анамалія (на малюнку пазначана $\nu$, таксама пазначаецца Шаблон:Math, $\theta$ ці Шаблон:Math) гэта вугал паміж радыус-вектарам Шаблон:Math цела і кірункам на перыцэнтр.

Сярэдняя анамалія (звычайна пазначаецца Шаблон:Math) для цела, што рухаецца па няўзбуранай арбіце, — здабытак яго сярэдняга руху (сярэдняй вуглавой скорасці за адзін абарот) і інтэрвалу часу пасля праходжання перыцэнтра. Іншымі словамі, сярэдняя анамалія — вуглавая адлегласць ад перыцэнтра да ўяўнага цела, якое рухаецца з пастаяннай вуглавой скорасцю, роўнай сярэдняму руху рэальнага цела, і праходзіць праз перыцэнтр адначасова з рэальным целам.

Эксцэнтрычная анамалія (пазначаецца Шаблон:Math) — параметр, які выкарыстоўваецца для выражэння пераменнай даўжыні радыус-вектара Шаблон:Math.

Залежнасць Шаблон:Math ад Шаблон:Math і $\nu$ выражаецца ўраўненнямі

$r=a(1-e\cdot \cos E),$

$r=\frac{a(1-e^2)}{1+e\cdot \cos \nu }$,

дзе:

• Шаблон:Math — вялікая паўвось эліптычнай арбіты;
• Шаблон:Math — эксцэнтрысітэт эліптычнай арбіты.

Сярэдняя анамалія і эксцэнтрычная анамалія звязаны паміж сабой праз ураўненне Кеплера.

Аргумент шыраты

Аргумент шыраты (пазначаецца Шаблон:Math) — вуглавы параметр, які вызначае становішча цела, што рухаецца ўздоўж кеплеравай арбіты. Гэта сума сапраўднай анамаліі (гл. вышэй) і аргумента перыцэнтра, які ўтварае вугал паміж радыус-вектарам цела і лініяй вузлоў. Адлічваецца ад узыходнага вузла па кірунку руху.

$u=\nu +\omega ,$

дзе:

• Шаблон:Math — аргумент шыраты;
• $\nu$ — сапраўдная анамалія;
• $\omega$ — аргумент перыцэнтра.

Анамалістычны перыяд абарачэння

Анамалістычны перыяд абарачэння — прамежак часу, за які цела, перамяшчаючыся па эліптычнай арбіце, двойчы паслядоўна праходзіць праз перыцэнтр.

Спасылкі

• Шаблон:ВТ-ЭСБЕ