Тэарэма Беры — Эсеена

У тэорыі імавернасцей цэнтральная лімітавая тэарэма сцвярджае, што пры пэўных умовах размеркаванне імавернасцей сярэдняга значэння выпадковай выбаркі Шаблон:Нп3 к нармальнаму размеркаванню пры нарастанні аб'ёму выбаркі да бесканечнасці. Пры больш моцных дапушчэннях, тэарэма Беры — Эсеена (або няроўнасць Беры — Эсеена) колькасна ацэньвае скорасць, з якою гэта збежнасць адбываецца, даючы ацэнку найбольшай пагрэшнасці прыбліжэння сапраўднага размеркавання нармальным. Прыбліжэнне ацэньваецца па адлегласці Калмагорава — Смірнова. У выпадку незалежных выбарак скорасць збежнасці мае парадак Шаблон:Math, дзе Шаблон:Math — аб'ём выбаркі, а пастаянная ацэньваецца праз трэція абсалютныя нарміраваныя моманты.

Сцвярджэнне тэарэмы

Фармулёўкі тэарэмы могуць адрознівацца, бо яна была адкрыта незалежна двума матэматыкамі: Эндру Беры (у 1941) і Шаблон:Нп3 (1942), які затым, разам з іншымі аўтарамі, некалькі разоў паляпшаў тэарэму на працягу наступных дзесяцігоддзяў.

Аднолькава размеркаваныя складнікі

Адзін з варыянтаў, які ў нечым ахвяруе агульнасцю дзеля яснасці, гучыць наступным чынам:

Няхай X₁, X₂, …, — незалежныя і аднолькава размеркаваныя выпадковыя велічыні з E(X_i) = 0, E(XШаблон:Su) = σ² > 0, і E(|X_i|³) = ρ < ∞. Вызначым выбарачнае сярэдняе:

$Y_n=\frac{X_1+X_2+\cdots +X_n}{n}.$

Няхай F_n ёсць функцыя размеркавання велічыні

$\frac{Y_n\sqrt{n}}{\sigma },$

а Φ ёсць функцыя стандартнага нармальнага размеркавання.

Тады існуе дадатная пастаянная C такая, што для ўсіх x і n справядліва няроўнасць

$|F_n(x)-\mathrm{\Phi }(x)|\le \frac{C\rho }{{\sigma }^3\sqrt{n}}.(1)$

Ілюстрацыя рознасці паміж упамянутымі ў тэарэме функцыямі размеркавання.

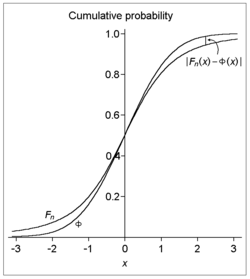
Гэта значыць: зададзена паслядоўнасць Шаблон:Нп3 з нулявым спадзяваннем і дадатнаю дысперсіяй, і, акрамя таго, з канечным трэцім абсалютным момантам. Тады функцыі размеркавання ўнармаванага выбарачнага сярэдняга і стандартнай нармальнай велічыні адрозніваюцца не больш чым на вызначаную велічыню. Варта заўважыць, што хібнасць прыбліжэння для ўсіх n абмежавана велічынёю парадку n^−1/2.

На працягу гадоў вылічаныя значэнні пастаяннай C прыкметна панізіліся са значэння 7.59, атрыманага ЭсеенамШаблон:Sfn, да 0.7882, атрыманага ван-БеекамШаблон:Sfn, пасля 0.7655Шаблон:Sfn, тады 0.7056Шаблон:Sfn, затым 0.7005Шаблон:Sfn, потым 0.5894Шаблон:Sfn, пазней 0.5129Шаблон:Sfn, затым 0.4785Шаблон:Sfn. Падрабязны агляд можна знайсці ў артыкулахШаблон:SfnШаблон:Sfn. Найлепшая ацэнка на 2012 год, C < 0.4748, вынікае з няроўнасці

$\underset{x\in ℝ}{\sup }|F_n(x)-\mathrm{\Phi }(x)|\le \frac{0.33554(\rho +0.415{\sigma }^3)}{{\sigma }^3\sqrt{n}},$

даказанай ШаўцовайШаблон:Sfn, пры ўліку суадносін σ³ ≤ ρ і 0.33554 · 1.415 < 0.4748. Аднак, калі ρ ≥ 1.286σ³, тады ацэнка

$\underset{x\in ℝ}{\sup }|F_n(x)-\mathrm{\Phi }(x)|\le \frac{0.3328(\rho +0.429{\sigma }^3)}{{\sigma }^3\sqrt{n}},$

якая таксама даказана ШаўцовайШаблон:Sfn, дае яшчэ стражэйшую верхнюю ацэнку.

ЭсеенШаблон:Sfn атрымаў ніжнюю мяжу для пастаяннай

$C\ge \frac{\sqrt{10}+3}{6\sqrt{2\pi }}\approx 0.40973\approx \frac{1}{\sqrt{2\pi }}+0.01079.$

Рознаразмеркаваныя складнікі

Няхай X₁, X₂, …, — незалежныя выпадковыя велічыні з E(X_i) = 0, E(X_i²) = σ_i² > 0, і E(|X_i|³) = ρ_i < ∞. Таксама няхай

$S_n=\frac{X_1+X_2+\cdots +X_n}{\sqrt{{\sigma }_1^2+{\sigma }_2^2+\cdots +{\sigma }_n^2}}$

унармаваная n-я частковая сума. Абазначым F_n функцыю размеркавання велічыні S_n, а сімвалам Φ — функцыю стандартнага нармальнага размеркавання. Дзеля зручнасці абазначым

$\overrightarrow{\sigma }=({\sigma }_1,...,{\sigma }_n),\overrightarrow{\rho }=({\rho }_1,...,{\rho }_n).$

У 1941 Эндру Беры даказаў, што для ўсіх n існуе абсалютная пастаянная C₁, такая што

$\underset{x\in ℝ}{\sup }|F_n(x)-\mathrm{\Phi }(x)|\le C_1\cdot {\psi }_1,(2)$

дзе

${\psi }_1={\psi }_1(\overrightarrow{\sigma },\overrightarrow{\rho })=(\sum _{i=1}^n{\sigma }_i^2{)}^{-1/2}\cdot \underset{1\le i\le n}{\max }\frac{{\rho }_i}{{\sigma }_i^2}.$

Незалежна, у 1942 годзе, Карл Густаў Эсеен даказаў, што для любых n існуе абсалютная пастаянная C₀, такая што

$\underset{x\in ℝ}{\sup }|F_n(x)-\mathrm{\Phi }(x)|\le C_0\cdot {\psi }_0,(3)$

дзе

${\psi }_0={\psi }_0(\overrightarrow{\sigma },\overrightarrow{\rho })=(\sum _{i=1}^n{\sigma }_i^2{)}^{-3/2}\cdot \sum _{i=1}^n{\rho }_i.$

Лёгка пераканацца, што ψ₀≤ψ₁. Таму няроўнасць (3) прынята называць няроўнасцю Беры-Эсеена, велічыня ψ₀ называецца дробам Ляпунова трэцяга парадку. Больш таго, у выпадку, калі ўсе складнікі X₁,… X_n размеркаваны аднолькава

${\psi }_0={\psi }_1=\frac{{\rho }_1}{{\sigma }_1^3\sqrt{n}},$

ацэнкі з няроўнасцей (1), (2) і (3) супадаюць.

Адносна C₀, відавочна, ніжняя мяжа, устаноўленая ЭсеенамШаблон:Sfn, застаецца ў сіле:

$C_0\ge \frac{\sqrt{10}+3}{6\sqrt{2\pi }}=0.4097\dots .$

Верхнія межы для C₀ пазней былі паніжаны ад зыходнай ацэнкі 7.59 ЭсеенаШаблон:Sfn да (тут пералічваюцца толькі нядаўнія вынікі) 0.9051 ЗалатароваШаблон:Sfn, 0.7975 ван-БеекаШаблон:Sfn, 0.7915 ШыганаваШаблон:Sfn, 0.6379 і 0.5606 ЦюрынаШаблон:SfnШаблон:Sfn. На 2011 год найлепшая ацэнка 0.5600 атрымана ШаўцовайШаблон:Sfn.

Гл. таксама

• Цэнтральная гранічная тэарэма
• Шаблон:Нп3
• Шаблон:Нп3

Літаратура

• Шаблон:Cite journal
• Durrett, Richard (1991). Probability: Theory and Examples. Pacific Grove, CA: Wadsworth & Brooks/Cole. ISBN 0-534-13206-5.
• Шаблон:Cite journal
• Шаблон:Cite journal
• Feller, William (1972). An Introduction to Probability Theory and Its Applications, Volume II (2nd ed.). New York: John Wiley & Sons. ISBN 0-471-25709-5.
• Шаблон:Cite journal
• Шаблон:Cite journal
• Manoukian, Edward B. (1986). Modern Concepts and Theorems of Mathematical Statistics. New York: Springer-Verlag. ISBN 0-387-96186-0.
• Serfling, Robert J. (1980). Approximation Theorems of Mathematical Statistics. New York: John Wiley & Sons. ISBN 0-471-02403-1.
• Шаблон:Cite journal
• Шаблон:Cite journal
• Шаблон:Cite journal
• Шаблон:Cite arXiv
• Шаблон:Cite journal
• Шаблон:Cite journal
• Шаблон:Cite journal
• Шаблон:Cite journal
• Шаблон:Cite journal

Спасылкі

• Шаблон:SpringerEOM